LRU & LFU

LRU 基础

内存的数据是有限的，因此不可能无限制地添加数据。假定我们设置缓存能够使用的内存大小为 N，那么在某一个时间点，添加了某一条缓存记录之后，占用内存超过了 N，这个时候就需要从缓存中移除一条或多条数据了。那移除谁呢？我们肯定希望尽可能移除“没用”的数据，那如何判定数据“有用”还是“没用”呢？

FIFO/LFU/LRU 算法简介

FIFO(First In First Out)

先进先出，也就是淘汰缓存中最老(最早添加)的记录。FIFO 认为，最早添加的记录，其不再被使用的可能性比刚添加的可能性大。这种算法的实现也非常简单，创建一个队列，新增记录添加到队尾，每次内存不够时，淘汰队首。但是很多场景下，部分记录虽然是最早添加但也最常被访问，而不得不因为呆的时间太长而被淘汰。这类数据会被频繁地添加进缓存，又被淘汰出去，导致缓存命中率降低。

LFU(Least Frequently Used)

最少使用，也就是淘汰缓存中访问频率最低的记录。LFU 认为，如果数据过去被访问多次，那么将来被访问的频率也更高。LFU 的实现需要维护一个按照访问次数排序的队列，每次访问，访问次数加1，队列重新排序，淘汰时选择访问次数最少的即可。LFU 算法的命中率是比较高的，但缺点也非常明显，维护每个记录的访问次数，对内存的消耗是很高的；另外，如果数据的访问模式发生变化，LFU 需要较长的时间去适应，也就是说 LFU 算法受历史数据的影响比较大。例如某个数据历史上访问次数奇高，但在某个时间点之后几乎不再被访问，但因为历史访问次数过高，而迟迟不能被淘汰。

LRU(Least Recently Used)

最近最少使用，相对于仅考虑时间因素的 FIFO 和仅考虑访问频率的 LFU，LRU 算法可以认为是相对平衡的一种淘汰算法。LRU 认为，如果数据最近被访问过，那么将来被访问的概率也会更高。LRU 算法的实现非常简单，维护一个队列，如果某条记录被访问了，则移动到队尾，那么队首则是最近最少访问的数据，淘汰该条记录即可。

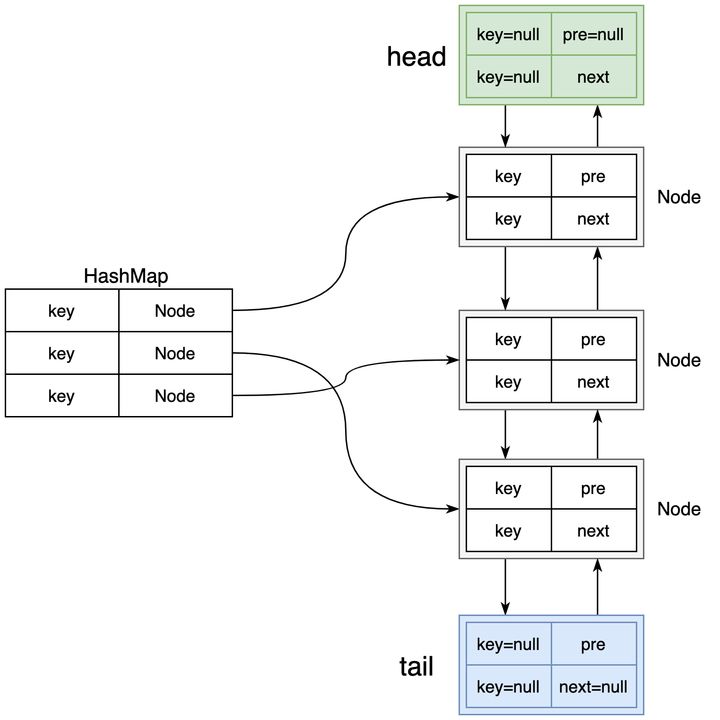
实现一个 LRU 需要用到一个哈希表和一个双向链表。

双向链表按照被使用的顺序存储了这些键值对，靠近头部的键值对是最近使用的，而靠近尾部的键值对是最久未使用的。
哈希表即为普通的哈希映射（HashMap），通过缓存数据的键映射到其在双向链表中的位置。
LRU 要点：删除都在表尾，添加都在表头，维护 dummy_head 和 dummy_tail ，
- 成员变量： cache, size, capacity; 头尾指针｜如果用list，自带head和tail
- 方法：
  - 1. 创建节点(到头); 删除一个节点
    2. 访问一个节点(原来位置的node 删除，把node移动到头) ; 删除尾部 (optional)

struct DLinkedNode {
    int key, value;
    DLinkedNode* prev;
    DLinkedNode* next;
    DLinkedNode(): key(0), value(0), prev(nullptr), next(nullptr) {}
    DLinkedNode(int _key, int _value): key(_key), value(_value), prev(nullptr), next(nullptr) {}
};

class LRUCache {
private:
    unordered_map<int, DLinkedNode*> cache;
    DLinkedNode* head;
    DLinkedNode* tail;
    int size;
    int capacity;

public:
    LRUCache(int _capacity): capacity(_capacity), size(0) {
        // 使用伪头部和伪尾部节点
        head = new DLinkedNode();
        tail = new DLinkedNode();
        head->next = tail;
        tail->prev = head;
    }
    
    int get(int key) {
        if (!cache.count(key)) {
            return -1;
        }
        // 如果 key 存在，先通过哈希表定位，再移到头部
        DLinkedNode* node = cache[key];
        moveToHead(node);
        return node->value;
    }
    
    void put(int key, int value) {
        if (!cache.count(key)) {
            // 如果 key 不存在，创建一个新的节点
            DLinkedNode* node = new DLinkedNode(key, value);
            // 添加进哈希表
            cache[key] = node;
            // 添加至双向链表的头部
            addToHead(node);
            ++size;
            if (size > capacity) {
                // 如果超出容量，删除双向链表的尾部节点
                DLinkedNode* removed = removeTail();
                // 删除哈希表中对应的项
                cache.erase(removed->key);
                // 防止内存泄漏
                delete removed;
                --size;
            }
        }
        else {
            // 如果 key 存在，先通过哈希表定位，再修改 value，并移到头部
            DLinkedNode* node = cache[key];
            node->value = value;
            moveToHead(node);
        }
    }

    void addToHead(DLinkedNode* node) {
        node->prev = head;
        node->next = head->next;
        head->next->prev = node;
        head->next = node;
    }
    
    void removeNode(DLinkedNode* node) {
        node->prev->next = node->next;
        node->next->prev = node->prev;
    }

    void moveToHead(DLinkedNode* node) {
        removeNode(node);
        addToHead(node);
    }

    DLinkedNode* removeTail() {
        DLinkedNode* node = tail->prev;
        removeNode(node);
        return node;
    }
};

使用 std::list 实现LRU，

#include <iostream>
#include <unordered_map>
#include <list>

using namespace std;


class LRUCache {
private:
    int capacity;
    unordered_map<int, pair<int, list<int>::iterator>> cache; // 存储键值对和对应在队列中的迭代器
    list<int> recent; // 存储最近使用的键，队首为最近使用的键，队尾为最久未使用的键

public:
    LRUCache(int capacity) {
        this->capacity = capacity;
    }
    
    int get(int key) {
        if (cache.find(key) != cache.end()) { // 如果缓存中存在该键
            updateRecent(key); // 更新最近使用情况
            return cache[key].first; // 返回键对应的值
        }
        return -1; // 如果缓存中不存在该键，返回-1
    }
    
    void put(int key, int value) {
        if (cache.find(key) != cache.end()) { // 如果缓存中已经存在该键
            updateRecent(key); // 更新最近使用情况
            cache[key].first = value; // 更新值
        } else {
            if (cache.size() >= capacity) { // 如果缓存已满
                evict(); // 淘汰最久未使用的键
            }
            recent.push_front(key); // 将新键加入队首
            cache[key] = {value, recent.begin()}; // 将键值对存入哈希表
        }
    }
    
private:
    void updateRecent(int key) {
        recent.erase(cache[key].second); // 从队列中删除原位置
        recent.push_front(key); // 将该键移到队首
        cache[key].second = recent.begin(); // 更新在队列中的位置迭代器
    }
    
    void evict() {
        int evictKey = recent.back(); // 获取最久未使用的键
        cache.erase(evictKey); // 从哈希表中删除该键
        recent.pop_back(); // 从队列尾部淘汰该键
    }
};

int main() {
    LRUCache cache(2); // 创建容量为2的LRU缓存
    
    cache.put(1, 1); // 缓存中：{1=1}
    cache.put(2, 2); // 缓存中：{1=1, 2=2}
    cout << cache.get(1) << endl;    // 返回 1
    cache.put(3, 3); // 缓存中：{1=1, 3=3}
    cout << cache.get(2) << endl;    // 返回 -1 (未找到)
    cache.put(4, 4); // 缓存中：{3=3, 4=4}，移除键 1
    cout << cache.get(1) << endl;    // 返回 -1 (未找到)
    cout << cache.get(3) << endl;    // 返回 3
    cout << cache.get(4) << endl;    // 返回 4
    return 0;
}

LRU 实现注意：

不要忘记及时更新map，map这里最好用emplace, 不要用[]来添加元素
双向链表把节点添加到head需要4步
put时元素若存在，也需要更新它的value
我的写法：两种成员方法， add2head（非新节点要把老位置的删掉）和 evict(删除节点）就够了

深入理解 LRU

LRU-K & 2Q

LRU算法实现虽然简单，并且在大量频繁访问热点页面时十分高效，但同样也有一个缺点，就是如果该热点页面在偶然一个时间节点被其他大量仅访问了一次的页面所取代，那自然造成了浪费。

LRU-K中的K代表最近使用的次数，因此LRU可以认为是LRU-1。

LRU-K的主要目的是为了解决LRU算法缓存污染的问题，其核心思想是将“最近使用过1次”的判断标准扩展为“最近使

用过K次”。

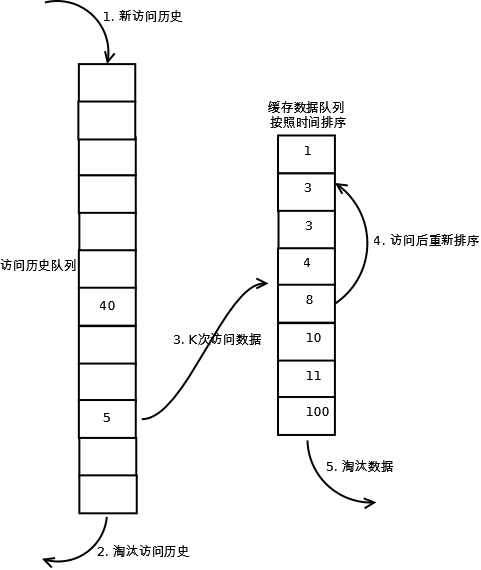
LRU 需要维护两个队列：历史队列和缓存队列。

历史队列保存着每次访问的页面，当页面访问次数达到了k次，该页面出栈，并保存至缓存队列；若尚未达到k次则继续保存，直至历史队列也满了，那就根据一定的缓存策略(FIFO、LRU、LFU)进行淘汰。
缓存队列则是保存已经访问k次的页面，当该队列满了之后，则淘汰最后一个页面，也就是第k次访问距离现在最久的那个页面。

简单来说，如果历史队列中的元素被访问了 K 次，它会离开历史队列前往缓存队列。缓存队列的元素就没那么容易被随便淘汰，抗干扰能力就强一些。

LRU workflow

LRU-K的历史队列和缓存队列在满时的更新策略可以自由选择
LFU 可以理解为 k = ∞ 的 LRU-K 算法。
2Q 算法是一种具体的 LRU-2 算法，其历史队列采用FIFO，缓存队列采用LRU-1。
LRU-K的性能：K = 2可能是最常用也最好用的。

redis 的 LRU 实现

由于 LRU 算法需要用链表管理所有的数据，会造成大量额外的空间消耗。

除此之外，大量的节点被访问就会带来频繁的链表节点移动操作，从而降低了 Redis 性能。

所以 Redis 对该算法做了简化，Redis LRU 算法并不是真正的 LRU，Redis 通过对少量的 key 采样，并淘汰采样的数据中最久没被访问过的 key。

这就意味着 Redis 无法淘汰数据库最久前访问的数据

Redis LRU 算法可以更改样本数量来调整算法的精度，使其近似接近真实的 LRU 算法，同时又避免了内存的消耗，因为每次只需要采样少量样本，而不是全部数据。

LFU, Least Frequently Used

本质上就是访问次数最少的滚蛋，访问次数一样少的就按照时间来淘汰。所以每个node都需要一个时间戳和一个访问计数器。

法一（慢的很）：
用std::set 来充当AVL tree，每个节点创建 freq 和时间戳，重载一下operator，这时 set 就会默认按照 1.访问次数 2. 访问时间排序了

struct node
{
    int key, value, freq = 1, t;
    node(int k, int v, int f, int t): key(k), value(v), freq(f), t(t) {}
    // rhs => right hand side, 表示等式右边。类似的可定义lhs
    bool operator < (const node& rhs) const {
        return freq == rhs.freq ? t < rhs.t : freq < rhs.freq;
    }
};


class LFUCache {
private:
    set<node> s; // 前面写好了 operator，s里是有默认排序的
    unordered_map<int, node> cache; // key -> node{..info..}
    int capacity, time; // time 是以单次操作作为单位

public:
    LFUCache(int capacity) : capacity(capacity), time(0) {
        s.clear();
        cache.clear();    
    }
    
    int get(int key) {
        if (capacity == 0) return -1;
        time++;
        auto it = cache.find(key); // hash map的索引是需要时间的
        if (it == cache.end()) {return -1;}
        // key 存在
        auto cur_node = it->second;
        // 更新 avl tree set
        s.erase(cur_node);
        // key, value, freq = 1, t;
        cur_node.freq++;
        cur_node.t = time;
        s.insert(cur_node);
        it->second = cur_node;
        return cur_node.value;
    }
    
    void put(int key, int value) {
        time++;
        if (capacity == 0) {return;}
        auto it = cache.find(key);
        if (it == cache.end()) {
            // 必须先删除再创建，不然你创建的这个会马上被踢出去！
            if (s.size() == capacity) {
                cache.erase(s.begin()->key);
                s.erase(s.begin());
            }
            // key 不存在，创建
            node cur_node = node(key, value, 1, time);
            s.insert(cur_node);
            cache[key] = cur_node; 
            // cache.insert(make_pair(key, cur_node));
        } else {
            // key 存在, 更新
            auto cur_node = it->second;
            s.erase(cur_node);
            cur_node.freq++;
            cur_node.t = time;
            cur_node.value = value;
            s.insert(cur_node);
            it->second = cur_node;
        }
    }
};

LFU实现注意：

注意同时更新hash map，尽量用insert或者emplace来添加元素
用set来存node，在node的结构体里定义operator，这时set就是有序的
在添加node之前，先检查满了没，不要先插入再删除，这样会把刚刚添加的node踢掉

其他资料：

面试中的 LRU / LFU 的青铜与王者 https://halfrost.com/lru_lfu_interview/
https://segmentfault.com/a/1190000022558044

Operating system

#Operating system

LRU & LFU

https://www.mementos.top/2024/07/29/LRU & LFU/

作者

Natsumi

发布于

2024年7月29日

许可协议

blog 更新日志上一篇

VF3图同构算法下一篇